Blog de MQI - Bacharelado
Aula 23 - seg. 10/5
Na aula de hoje vimos:
- como aparecem e como resolvemos a eq. de Schrodinger quando o espaço de Hilbert tem dimensão finita. Começamos com um exemplo de Hamiltoniana para um sistema de 2 níveis.
- Voltamos a discutir o uso da notação de Dirac: operadores lineares, projetores, conjugado Hermitiano, decomposição espectral (problema 3.24 do Griffiths), problema 3.37 do Griffiths (sistema de 3 níveis).
Refs.: Griffiths seção 3.6.
Aula 22 - sex. 7/5
- Pacote de onda de incerteza mínima: vimos que são as gaussianas, como já tínhamos adiantado quando examinamos
e 
para o estado fundamental do OH. - Incerteza para energia/tempo: fórmula semelhante à de incerteza para x e p, mas com interpretações diferentes.
continua interpretada como o desvio-padrão das medidas de energia 
. 
não é o desvio-padrão de medidas de tempo, já que o tempo não é observável; está relacionado ao tempo para uma mudança significativa do sistema. Aqui vocês encontram um artigo de Paul Bush com um levantamento das dificuldades associadas à definição de um princípio de incerteza para tempo e energia. - 3 exemplos de aplicação do princípio de incerteza para tempo e energia.
- Notação de Dirac: vetores e operadores lineares (a continuar na próxima aula).
Refs.: Griffiths seções 3.5 e 3.5.
Aula 21 - ter. 4/5
- continuando o estudo da interpretação estatística generalizada: como recuperar a interpretação estatística para os operadores
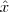e 
. - Exercícios: exemplo 3.4, problema 3.11.
- Princípio da Incerteza generalizado: derivação, como recuperamos o princípio de incerteza de Heisenberg para 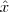e .
- Definindo a noção de observáveis compatíveis e incompatíveis a partir das relações de comutação.
Refs.: Griffiths seções 3.4 e 3.5. OBS.: A lista 5 já está disponível, a data de entrega é sexta-feira, 14/5.
Aula 20 - seg. 3/5
Continuamos estudando o cap. 3 do Griffiths.
- Autofunções de operadores Hermitianos: ortogonalidade e completeza no caso de espectro discreto.
- O caso de espectro contínuo: ortogonalidade (à la Dirac) e completeza. Estudamos somente os operadores momento e posição, o caso de espectro contínuo geral tem sutilezas, pois nem sempre as integrais que representam os produtos internos convergem…
- Interpretação estatística generalizada: como encontrar a probabilidade de medirmos qualquer valor de observável geral.
Refs.: Griffiths seções 3.3, 3.4.
Aula 19 - sex. 30/4
Continuamos estudando o formalismo da MQ: operadores, observáveis, etc.
- Estados bem-definidos: vimos que ter variância = 0 para um observável é equivalente a ser auto-estado deste observável.
- Exemplo 3.1: auto-estados do operador
. - Mais sobre auto-funções de operadores Hermitianos: começamos a estudar o caso de espectro discreto. Primeiro resultado: auto-valores são reais.
Refs.: Griffiths seções 3.2 e 3.3.
